Where the techniques of Maths
are explained in simple terms.
Calculus - Differentiation - Applied max/min questions.
Type 2: 2D shapes - Test Yourself 2.
- Algebra & Number
- Calculus
- Financial Maths
- Functions & Quadratics
- Geometry
- Measurement
- Networks & Graphs
- Probability & Statistics
- Trigonometry
- Maths & beyond
- Index
| The questions on this page focus on situations: |
| 1. creating two shapes. |
| 2. addressing areas including paddocks, etc |
| 3. involving geometric shapes. |
| 4. measuring the distance between two curves. |
| Creating 2 shapes. |
1. Two circles with radii x and y are such that the sum of their radii has a constant value R.
Answer.Min area = (πR2)/2. |
| 2. A wire of length 24 cm is cut into two pieces. One piece is then bent to form a square with sides a cm. The other piece is bent to form an equilateral triangle with each side of length b cm.
Let AS be the area of the square and AT be the area of the triangle.
|
|
| Areas and paddocks. | 3. In the diagram below, P is a point on the curve y = x(6 - x) and Q is a point on the curve y = x(x - 4). PQ cuts the x axis at right angles at R.
Answer.Max area = 37.04 u2. |
| 4. A flag has two vertical green stripes at the ends and a vertical yellow stripe in the centre. The design and measurements are shown below:
Answer.Dimensions are 81.04 × 106.96. |
|
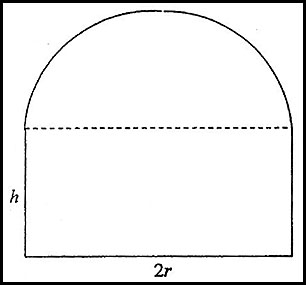
| 5. Robin has designed a garden bed which consists of a rectangle and a semicircle as shown in the diagram.
The perimeter of Robin's garden is 20 m. Answer.(i) h = 10 - r - πr/2 (iii) r = 20/(4 + π) = 2.8. Area = 28 m2. |
|
| 6. The diagram shows a triangular piece of land ABC with dimensions BC = a metres, AC = b metres and AB = c metres (where a ≤ b ≤ c).
The owner of the land wants to build a straight fence to divide the land into two pieces of equal area. Let S and T be points on AB and AC respectively so that ST divides the land as intended. Let AS = x metres, AT = y metres and ST = z metres.
|
|
7. In the diagram below, the point  is a variable point on the curve is a variable point on the curve  . .
The points S (-5, 2) and T (3, -4) lie on the straight line 3x + 4y + 7 = 0.
|
|
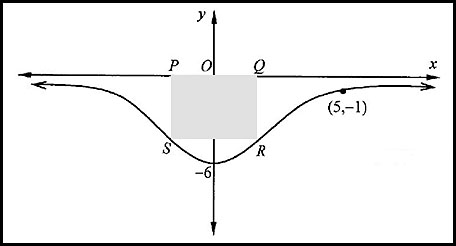
8. In the diagram below, the curve 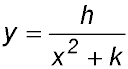 (where h and k are constants) has a minimum turning point at (0, -6) and it passes through the point (5, -1). (where h and k are constants) has a minimum turning point at (0, -6) and it passes through the point (5, -1).
A rectangle PQRS is inscribed within the curve as shown with its axis of symmetry
|
|
| Geometric shapes. | 9. The diagram above represents the dimensions (in metres) of a small garden. Answer.The minimum perimeter is 14.47 m. |
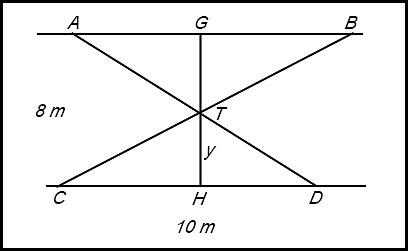
| 10. In the diagram below, AB and CD are parallel railings which are 8 m apart.
The points C and D are 10 m apart on the lower railing. Two crossbars AD and BC intersect at T as shown. The line through T perpendicular to AB intersects AB at G and CD at H. The length of TH is y metres.
Answer.For min area, y = 8 cm. |
|
11. The parabola y = 4 - x2 cuts the x-axis at R and S. The point P (x, y) lies on the parabola in the first quadrant. Q also lies on the parabola such that PQ is parallel to the x-axis.
|
|
| 12. A circular window of radius√5 m requires three metal strips AB, DC and FG for reinforcement as shown in the diagram below. O is the centre of the window. OF = OG = y metres and FB = FA = CG = GD = x metres.
Answer.Max L when x = 2 m. |
|
13. An isosceles trapezium is inscribed in a semi-circle of radius R. The longer parallel side of the trapezium forms the diameter of the semi-circle. Show that the length of the shorter parallel side of the trapezium equals the radius of the semi-circle when the area of the trapezium is a maximum.(You can assume the concavity is negative). |
|
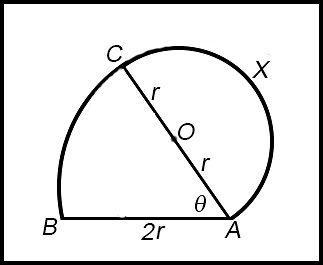
| 14. The cross-section of a metal cam is shown in the diagram below.
The cross-section consists of a semi-circle AXC centered at O with radius r cm and a sector ABC of radius 2r cm centered at A with angle θ. (i) What is the perimeter of the metal cam in terms of r and θ? (ii) If the area of the cross-section is fixed at 4 cm2, show that the perimeter in part (i) can be expressed as
(iii) Show that the perimeter in part (i) is smallest when |
|
| Distance between 2 curves. | 15. P is a point on the curve y = x(6 - x) and Q is a point on the curve y = x(x - 4).
Answer.Min length is 12.5 u. |
16. |
 .
. .
. .
.

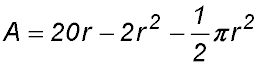

 .
.
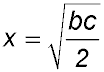 .
.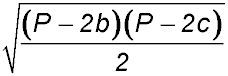 where
where 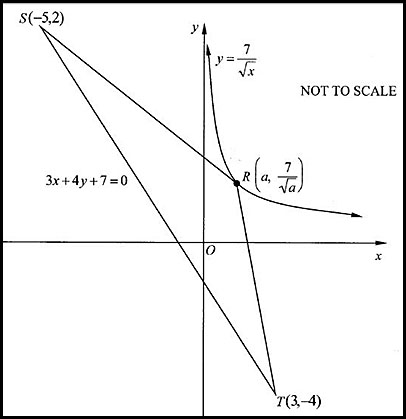
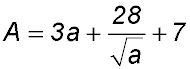 .
. 
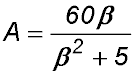 .
.


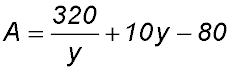

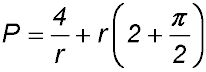
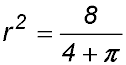 .
.